金属导热理论的研究进展与前沿问题

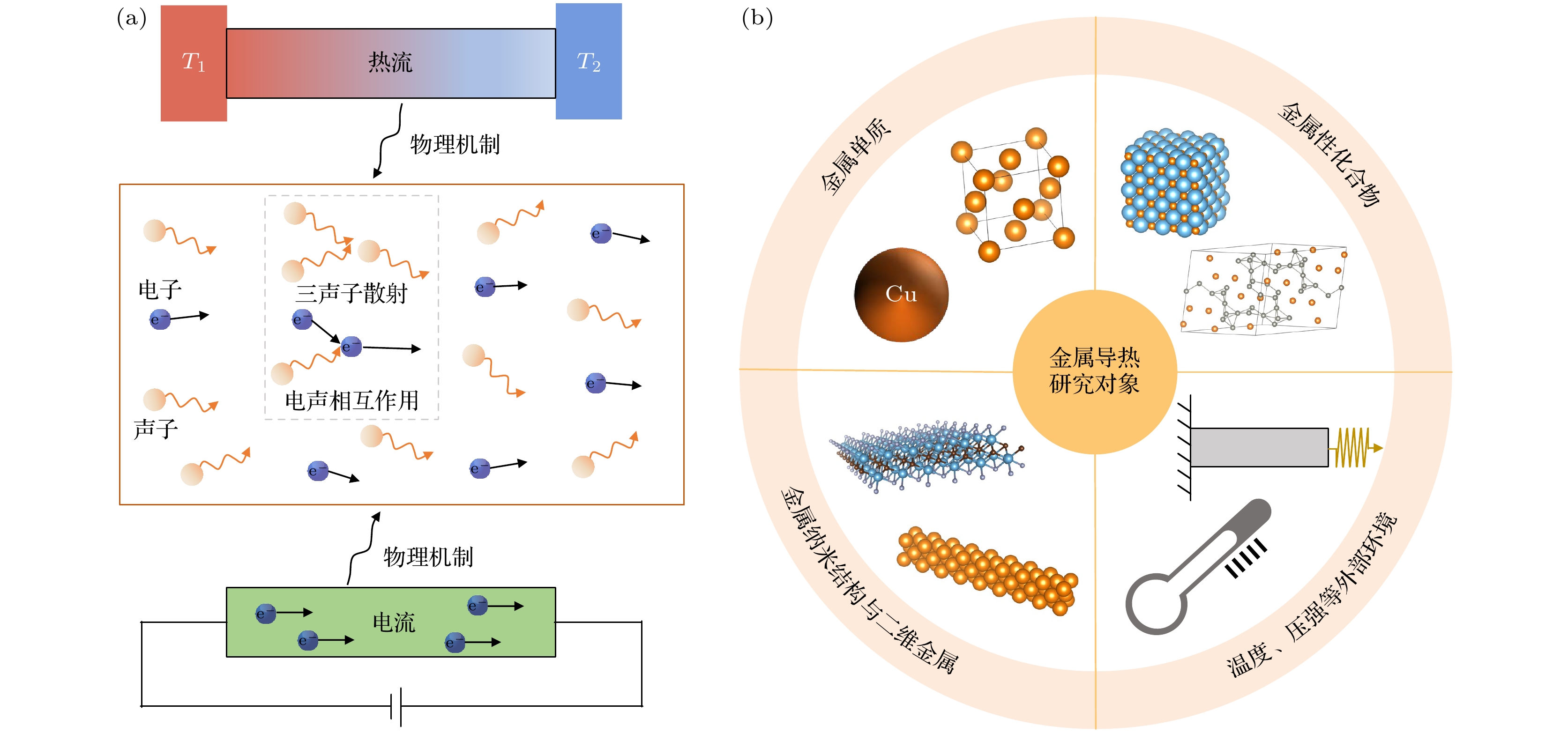
1.   引　言

金属材料是人类使用的最广泛的材料之一. 在诸多应用场景下, 例如换热器[1,2]、电子封装等[3]、金属的导热性能至关重要. 另一方面, 从基本的固体理论的角度来说, 金属的导热理论也是固体物理学的重要分支[4]. 因此, 对金属的导热性能研究在工程和理论方面都具有重要意义. 目前, 对金属导热机理的理解仍主要基于一百多年前的威德曼-弗朗兹定律[5,6](Wiedemann-Franz law). 该定律指出, 金属的热导率κ$�$与电导率σ$�$之间成正比关系, 即κ/σ=LT$�/�=��$, 其中L为洛伦兹常数, 而T为温度[5,6]. 金属电导率和热导率的正比关系最早在1853年被威德曼和弗朗兹通过实验发现[7]. 1881年, Lorenz [8]优化了该实验定律, 并提出金属热导率与电导率和温度的乘积成正比. 1900年, Drude [9]基于自由电子气模型推导出了这一比例系数, 得到的数值为1.11×10–8 W·Ω·K–2, 这一结果远低于实验测量值. 1928年Sommerfeld [10]基于量子力学模型重新推导, 得到了与实验吻合良好的比例系数, 即理论标准洛伦兹数L0 = 2.44×10–8 W·Ω·K–2 (Sommerfeld value)[10]. 该理论获得了极大的成功, 可以解释多数常见金属的实验测量结果. 例如铜的洛伦兹数为2.31×10–8 W·Ω·K–2 [6], 铝的洛伦兹数为2.10×10–8 W·Ω·K–2 [6]. 然而, 推导出上述标准洛伦兹数需要一些基本假设, 包括: 电子必须为完全的自由电子; 电子在导电和导热过程的散射机制必须完全一致; 晶格导热贡献必须远小于电子导热. 上述条件在绝大多数金属中都不是严格成立的. 事实上, 实验上也发现了部分金属的洛伦兹数与标准值存在显著偏差, 如钨的洛伦兹数为3.27×10–8 W·Ω·K–2[6], 远大于L0. 更多的实验结果表明, 不同材料室温下的实测洛伦兹数在L0的0.81倍到1.76倍之间[6]. 

从金属电子导热理论的建立到近年来, 对金属导热的研究相对较少. 在20世纪80年代前后, 部分工作对金属热导率进行了实验测量, 并试图从实验上分离金属中的电子和声子的导热贡献[11–15]. 理论方面在1958和1979年发展的Klemens模型[16]和Slack方程[17], 均只考虑了声子-声子非简谐相互作用而忽略了声子和电子的相互作用, 因而不适用于计算金属体系的声子热导率. 1986年Klemens和Williams [18]基于长波声子近似和自由电子气模型, 通过引入电声耦合常数项改进了原本用于半导体和绝缘体的声子导热解析模型, 并估算了多种单质金属的声子热导率. 然而, 金属导热中仍有一些基本问题没有得到很好的解决, 其中一个是声子导热在不同金属中的贡献大小问题, 另一个是威德曼-弗朗兹定律的成立条件. 文献[6,11,19]认为金属中的声子导热贡献不超过10%. 对于威德曼-弗朗兹定律的成立条件, 一般认为在室温区是成立的, 而在中低温区的结果表明洛伦兹数会明显的偏离L0[6,20,21]. 因为这些导热的基础理论问题未能得到完整的解决, 因此难以基于理论开展相关领域的工程问题, 如基于金属导热特性设计金属制备工艺. 

由于实验手段的限制, 特别是分离电子和声子导热具有现实上的困难, 上述问题很难通过实验手段回答. 近年来, 随着第一性原理计算方法的发展, 特别是基于EPW[22]的电子声子耦合计算理论工具的发展, 使得从量子力学基本原理出发计算热载流子的散射过程并结合玻尔兹曼输运方程计算电子和声子的热导率成为了可能. 过去十余年, 金属热导率的计算研究获得了显著的进展. 在各种理论方法中, 基于模态分析的方法成为了研究主流. 这一方法计算各个电子/声子模态的比热容、群速度和弛豫时间, 进而获得热导率[23–27]. 此方法不仅可以对热导率进行准确预测, 与此同时还包含了大量热载流子的微观信息, 为发掘深层次金属导热机制提供了工具. 金属导热的计算过程中最为关键的是量化金属中电子以及声子的散射过程. 多种散射源可以引起声子的散射, 例如声子-声子散射[28], 声子-电子散射(声电散射)[22], 声子-缺陷散射[29]等. 电子热输运中同样存在多种类型的散射, 例如电子-声子散射(电声散射)[30]、电子-电子散射[31]、电子-缺陷散射[32]等. 本文将主要关注三声子散射与电声和声电散射作用. 一方面已有大量的理论研究表明考虑这两种类型的散射作用可以得到与实验吻合良好的室温附近的热导率[25,33,34]. 另一方面针对其余的散射过程诸如电子-缺陷散射等, 现有的研究较少, 计算框架还不成熟, 有待未来进一步探索. 如图1(a)所示, 本文考虑了三声子散射与电声和声电散射机制. 金属导热的具体研究对象亦本文的整体结构如图1(b)所示. 本文将介绍最近十几年来, 针对这些研究内容和对象, 金属导热理论的研究进展和最新成果, 并探讨相关领域未来的研究方向和发展趋势. 

图 1  (a)金属导热与导电的微物理观过程示意图, 包括三声子散射和电声相互作用; (b)金属导热主要研究对象, 包括金属单质、金属性化合物、金属纳米结构与二维金属的导热, 以及金属导热受到不同外界因素诸如温度、压强等的影响

Fig. 1.  (a) Microscopic physical process of electron thermal transport and electrical transport, including three-phonon scattering and electron-phonon interaction; (b) the main research objects for thermal transport in metals, including the thermal transport in elemental metals, metallic compounds, metallic nanostructure, and two-dimensional metals; as well as the effect of external environments, such as temperature and pressure on thermal conductivity.

下载: 全尺寸图片 幻灯片

2.   金属导热特性以及电子和声子对导热的贡献

2.1   金属单质的导热

金属单质结构简单且应用场景广泛, 因而首先得到了大量的理论研究. 2016年Jain与McGaughey[25]对金、银、铝三种金属中的热导率进行了理论计算, 采用晶格动力学方法获得了三声子散射率, 密度泛函微扰理论获得声电散射率. 计算得到金、银、铝的热导率分别为278, 374, 252 W/(m·K), 和实验结果偏差均小于13%, 证明了本方法的合理性. 此外, 这一工作也讨论了声子导热的贡献, 并发现金、银、铝的室温声子热导率分别为2, 4, 6 W/(m·K). 这与半导体硅中140 W/(m·K)的声子热导率相比明显偏低, 这是因为相对硅而言, 金、银、铝中的声子散射通道较多, 化学键的非简谐性相对较强. 另一方面, 金、银、铝在室温下声子导热对热导率的贡献占比均小于3%, 相对电子导热贡献而言较低. 同年Wang等[35]针对金属中的声子导热问题, 继续对6种金属——金、银、铜、铝、铂、镍进行了理论计算. 通过对比分析, 他们发现金、银、铜、铝的声子热导率基本不受电子散射的影响, 而铂和镍的声子热导率则因声电散射的作用分别下降约20%和30%. 这是因为声电散射强度与费米能处的电子态密度直接相关, 声电散射中需要两个电子态参与, 且二者的动量差要等于参与散射声子的动量以满足守恒定律, 因此费米能处电子态密度高的金属中有更多的电子态满足散射动量关系, 增加声子的散射通道. 铂和镍在费米能处的电子态密度相对金、银、铜、铝而言较大, 因此声电散射较强. 2019年, Tong等[34]进一步探究了金属中的声子导热, 对11种典型单质金属进行了计算. 研究发现只考虑三声子散射时, 声子热导率为3—30 W/(m·K), 考虑声电散射后, 数值范围下降至3—18 W/(m·K). 整体上过渡金属中的声电散射对声子导热的抑制作用强于贵金属, 这是因为过渡金属中费米能处的电子态密度较大且声子频率较高. 电子导热方面, 锰与钛的电子热导率为5 W/(m·K)和25 W/(m·K), 其余金属单质的电子热导率普遍高于70 W/(m·K), 金、银、铜的电子热导率则是达到了273—451 W/(m·K). 基于计算获得的电子和声子的热导率, 如图2(a)所示, 该研究进一步发现, 这些单质金属中的声子导热占总热导率的1%—40%. 此外, 这一工作也计算了电导率并确定了洛伦兹数. 除了钯、镍、锰的室温洛伦兹数偏离标准值28%, 24%, 14%, 其余单质金属的洛伦兹数相对标准值的偏离均不超过9%. 2019年, Chen等[24]则在计算中发现过渡金属钨的洛伦兹数要高于标准值30%. 如图2(b)所示, 这是因为其声子热导率为46 W/(m·K), 占总热导率的25%. 去除声子导热后的洛伦兹数则接近标准值. 他们同时发现, 与常规的声子热导率随温度呈反比例下降这一规律不同, 图2(b)中可见钨的声子热导率基本不随温度变化. 这是因为钨中的三声子散射弱于声电散射, 因此基本不随温度变化的声电散射主导了声子的导热. 2020年Wen等[36]在过渡金属钼中发现了相似的现象并得出相同的结论. 为了分析不同晶相对导热的影响, 2022年Li等[37]选取了六方相贵金属金、银、铜进行了计算. 该研究发现六方相金、银、铜的热导率接近于常见立方相, 约为200—280 W/(m·K), 且声子对导热的贡献小于5%. 综上所述, 在金属单质导热的研究中发现, 金、银、铜、铝中电子是主要的热载流子, 声子导热的贡献低于5%. 部分过渡金属如钨中声子导热对总热导率的贡献可达25%, 并导致洛伦兹数偏离标准值30%左右. 此外, 单质金属中费米面上的电子密度在一定程度上可反映声电散射对声子导热的作用强度. 

图 2  (a) 300 K下部分金属中电子与声子导热对总热导率的贡献占比[34]; (b) 200—500 K下钨的声子热导率、电子热导率及总热导率与实验的对比(上图), 考虑总热导率与只考虑电子热导率下钨的洛伦兹数(下图)[24], 虚线所示L0为标准洛伦兹数

Fig. 2.  (a) Percentage of electron and phonon thermal conductivity contributing to total thermal conductivity for several metals[34]. (b) The phonon, electron, and total thermal conductivity of tungsten compared with experiments from 200 to 500 K (upper panel); the Lorenz number of tungsten considering total thermal conductivity versus considering electronic thermal conductivity (lower panel) [24], the dashed line is the standard Lorenz number L0.

下载: 全尺寸图片 幻灯片

2.2   金属性化合物的导热

金属性化合物为两种及以上元素构成的金属性材料. 金属性化合物种类繁杂, 应用广泛, 但也正因其元素和结构种类多样, 其导热的物理机制更为复杂. 本节将介绍两种典型的金属性化合物导热的研究进展. 首先对金属间化合物的导热研究进行介绍. 金属间化合物是由多种金属元素组成的晶体, 它作为第2相普遍存在于合金中, 对合金的改性和导热起到重要作用[38]. 2018年Tong等[39]计算发现, NiAl和Ni3Al的导热机制类似. 图3(a)以NiAl为例, 展示了其100—1000 K下电子和声子热导率. NiAl在300 K下声子导热对热导率贡献占比约17%, 且这一比例随温度上升而下降. 此外, 该研究发现声电散射在声子导热中起到了重要作用. 在100 K下, 声电散射使得NiAl和Ni3Al的声子热导率分别下降55%和75%, 但高于600 K时, 声电散射对声子导热的作用则不明显. 2020年Giri等[33]计算了CuAu, Cu3Au和CuAu3的电子热导率, 并发现它们的数值低于单质Cu和Au, 且这3种Cu-Au金属间化合物的电声相互作用强度强于单质Cu和Au. 此外, 部分金属间化合物导热还呈现出了各向异性. 例如, 2020年Liu等[40]发现Cu-Al金属间化合的声子导热受各向异性的杨氏模量影响而呈现了各向异性; 2022年Daeumer等[41]则发现Cu-Sn金属间化合物的电子导热因各向异性的电子能带而呈现各向异性. 另一方面, 针对部分金属间化合物复杂原胞的情况, 2023年Wang等[42]对原胞内含超过十个原子的Mg-Zn金属间化合物MgZn2和Mg4Zn7进行了计算. 如图3(b)所示, 研究发现当金属间化合物的晶胞足够复杂时, 总热导率基本不随温度变化, 且300 K下声子对导热的贡献小于4%. 这一较低的声子导热贡献一方面是因为金属键相较共价键和离子键而言较弱, 另一方面因为与声子导热直接关联的声学德拜温度随元胞原子数增加而下降. 综上所述, 金属性化合物中的声子导热贡献占比与原胞的复杂度有关, 原胞相对简单的Ni-Al化合物在300 K下声子导热贡献为17%, 而在原胞多于十个原子的Mg-Zn化合物中, 300 K下声子的导热贡献则低于4%. 此外, 部分金属性化合物中声子和电子导热存在各向异性. 

图 3  (a) NiAl[39], (b) MgZn2和Mg4Zn7[42]中的声子热导率、电子热导率和总热导率随温度的变化

Fig. 3.  Variation of phonon thermal conductivity, electron thermal conductivity, and total thermal conductivity with temperature for (a) NiAl[39], (b) MgZn2 and Mg4Zn7[42].

下载: 全尺寸图片 幻灯片

金属性陶瓷(金属碳化物、氮化物和硼化物)是一种硬质耐高温材料, 适用于极端环境, 其导热性质对性能提升十分重要, 得到了学界广泛关注. 下面介绍金属性陶瓷的导热研究进展. 2018年Li等[43]发现NbC和TiC的声子热导率的温度依赖关系不同. 如图4(a)所示, TiC的声子热导率随温度增加而下降, 遵循常规的反比例规律, 而NbC的声子热导率则基本不随温度变化. 相比TiC, NbC中特殊的声子温度依赖关系是因为其声电散射较强而三声子散射较弱, 弱温度依赖的声电散射主导了声子的热输运过程. 从图4(a)还可以看出, NbC中三声子散射强度较弱, 体现在只考虑三声子散射和声子-同位素散射时, 其声子热导率为3000 W/(m·K), 远高于TiC中82 W/(m·K)的数值. 该研究分析表明这是因为Nb与C的原子质量差异大于Ti和C的质量差异, 导致了NbC中声子带隙相对较大, 因此NbC的声子散射相空间低于TiC. 另一方面, 声电散射对NbC声子热导率的影响明显强于TiC. NbC中较强的声电散射是因为其电子费米面为嵌套结构(nesting), 如图4(a)所示, 因此其声电散射相空间高于TiC. 这一工作进一步发现了VC和TaC中均存在类似于NbC的声子导热规律. 在随后2020年的一些研究中, 对于WC, MoC[44]以及金属氮化物TiN, HfN[45]和金属硼化物ZrB2, TiB2[46]这几种金属性陶瓷材料, 均发现了类似于NbC的声子导热规律, 并有着相同的机理. 此外, 2020年的部分工作中讨论了声子导热对总热导率的贡献占比. WC, NbC, TiN, HfN的[44,45]计算数据表明, 电子和声子的室温热导率分别处于43—69 W/(m·K)和20—131 W/(m·K)的范围, 声子导热对热导率的贡献为26%—74%. 为进一步分析金属陶瓷中的电子导热, 以TiN为例, 图4(b), (c)给出了其电子及声子热导率, 电导率和洛伦兹数的计算结果. 电子及总热导率基本不随温度变化. 使用总热导率计算洛伦兹数时, 室温数值将高于标准值60%左右. 而使用电子热导率计算洛伦兹数时, 室温洛伦兹数则高于标准值10%, 并随温度升高而升高, 最终平稳在1.3L0附近[45]. 基于以上对声子导热的物理理解, 2021年Kundu等[47]找到了一种具有高室温热导率(~1000 W/(m·K))的θ相TaN. 其三声子散射规律与NbC等金属陶瓷相似, 但因θ相TaN费米能处电子态密度趋近于零, 降低了声电散射相空间, 因此由声电散射引起的声子热导率下降不超过20%, 这也导致了θ相TaN具有较高的室温声子热导率. 2021年Liu等[48]发现六方NbN中室温声子热导率小于5 W/(m·K). 这是因为虽然Nb和N的原子质量有数倍的差异, 六方NbN声子谱的带隙却远低于NbC, 因此不同于NbC, 六方NbN中的三声子散射没有受到明显抑制. 综上所述, 在部分金属性陶瓷中发现了相似的物理现象: 三声子散射受到抑制, 声电散射使声子热导率数值有数量级的降低, 导致声子热导率基本不随温度变化. 金属性陶瓷中声子热输运对热导率可贡献26%—74%. 此外, 部分研究发现如果能减弱声电散射或增强三声子散射, 将会使声子热导率明显上升或下降. 

图 4  (a) 200—1000 K下只考虑声子-声子和声子-同位素散射(虚线), 与同时考虑声子-声子、声子-同位素散射和声电散射(实线)下NbC和TiN的声子热导率[43], 插图为二者的电子费米面; (b) 200—1000 K下TiN的声子热导率、电子热导率、总热导率随温度的变化[45]; (c) 200—1000 K下TiN的电导率与洛伦兹数随温度的变化[45]

Fig. 4.  (a) Phonon thermal conductivity for NbC and TiC limited by phonon-phonon and phonon-isotope scattering (dashed curve), phonon-phonon, phonon-isotope, and phonon-electron scattering (solid curve) from 200 to 1000 K[43]. Inset: The Fermi surfaces of NbC and TiC. (b) The phonon thermal conductivity, electron thermal conductivity, and total thermal conductivity of TiN from 200 to 1000 K[45]. (c) The Lorenz number of TiN from 200 to 1000 K[45].

下载: 全尺寸图片 幻灯片

表1列出了上述不同金属中的电子和声子热导率. 综合以上2.1和2.2节可见, 整体上金属的洛伦兹数偏离标准值的原因是高占比的声子导热. 而高占比声子导热的金属一般有两个特点, 即硬度较高和费米能处电子态密度较低. 同时满足这两个条件时, 三声子散射和声电散射同时受到抑制, 因此声子热导率数值和相对总热导率的占比高. 

表 1  金属中的电子与声子热导率

Table 1.  Electron and phonon thermal conductivity in metals.

金属	300 K下热导率/(W·m–1·K–1)			声子导热占比/%
	总热导率	电子热导率	声子热导率
Au	278[25]	276[25]	2[25]	0.7
Ag	374[25]	370[25]	4[25]	1.1
Al	252[25]	246[25]	6[25]	2.4
Cu	378.7[34]	361.3[34]	17.4[34]	4.6
Mn	8[34]	5[34]	3[34]	37.5
Ti	30.6[34]	25.3[34]	5.3[34]	17.3
W	186[24]	140[24]	46[24]	24.7
Mo	162[36]	125[36]	37[36]	22.8
hcp-Au (a-axis)	201.3[37]	199[37]	2.3[37]	1.1
hcp-Ag (a-axis)	276.6[37]	274[37]	2.6[37]	0.9
hcp-Cu (a-axis)	279.4[37]	270[37]	9.4[37]	3.4
NiAl	71[39]	59[39]	12[39]	16.9
Ni3Al	28[39]	22[39]	6[39]	21.4
MgZn2	53.9[42]	52[42]	1.9[42]	3.5
Mg4Zn7	21.9[42]	21.4[42]	0.5[42]	2.3
WC (a-axis)	177[44]	46[44]	131[44]	74.0
NbC	74[44]	43[44]	31[44]	41.9
TiN	69[45]	49[45]	20[45]	29.0
HfN	93[45]	69[45]	24[45]	25.8
θ-TaN (a-axis)	1031[47]	36[47]	995[47]	96.5
hcp-NbN	4.4[48]	1.5[48]	2.9[48]	65.9

下载: 导出CSV 

| 显示表格

2.3   金属纳米结构的导热

近些年来金属纳米结构(纳米薄膜与纳米线)在芯片, 微电子等领域得到广泛应用. 芯片散热对维持芯片性能与稳定性极为重要[49], 因此金属纳米结构的导热成为研究重点. 虽然金属纳米薄膜与纳米线有着不同的工程应用, 但二者的导热都同样受晶界、边界等散射过程的影响, 有类似的物理规律, 因此本文重点以金属薄膜为例进行讨论和总结. 纳米尺度下, 金属的导热和导电现象会出现尺寸效应, 即金属热导率和电导率会随尺寸下降而下降. 理论上一般认为这是由于表面和晶界对电子和声子的散射[50,51]. 1970年Mayadas和Shatzkes[52]建立了金属纳米薄膜中电导率尺寸效应的模型(MS模型), 这一模型后续也被用于理解金属纳米结构中热导率的尺寸效应. Nath等[53]和Kelemen[54]分别于1974和1976年测量了铜纳米薄膜的热导率, 发现了热导率的尺寸效应. 1994年Kumar等[55]通过求解玻尔兹曼方程发现, 室温下只存在边界散射效应时, 在薄膜厚度低于电子平均自由程15倍时出现尺寸效应; 当存在晶界散射时, 这一临界尺寸变为电子平均自由程的50倍. 21世纪初, Feng等[56]通过统计方法计算了表面和晶界对电子的散射过程, 计算了300 K下铜纳米薄膜热导率随厚度的关系, 结果与Nath等[53]、Kelemen[54]的测量结果, 以及Kumar等[55]的计算结果进行了对比, 如图5(a)所示计算和实验的规律一致且吻合良好. 最近20年金纳米结构热导率在实验上受到了更多的关注. 2006年, Zhang等[57]采用直流电加热法测量了21—37 nm厚的金纳米薄膜热导率, 发现300 K下的热导率为160—180 W/(m·K). 这一工作将测得的电导率和热导率分别拟合MS模型, 发现晶界散射系数在传热过程中为0.25, 而在导电过程中则为0.7. 2013年Lin等[58]测量了6.4 nm厚的金薄膜的热导率, 发现热导率为61.9 W/(m·K), 相比体块结构下降了80.5%. 2019年Sawtelle和Reed[59]结合了自热法和自由电子模型, 通过实验测量的电导率估算了直径为24, 40, 53 nm的金纳米线的热导率, 发现200 K下热导率在6—18 W/(m·K)范围内. 2020年Mason等[60]测量了19—372 nm厚度的金薄膜热导率, 发现室温热导率范围约为70—95 W/(m·K). 除上述热导率尺寸效应的研究外, 也有较多关于金属纳米结构中的洛伦兹数的研究. 2010年Stojanovic等[61]将MS模型扩展到方形金属纳米线上, 定量地研究了常见金属纳米线的热导率和洛伦兹数, 发现洛伦兹数偏离标准值是声子和非弹性声电散射共同导致的. 例如, 室温下截面边长为300 nm的金纳米线的导热中声子贡献约为2%, 其洛伦兹数接近标准值; 而同样尺寸的钨纳米线中声子导热贡献占比约为30%, 其洛伦兹数高于标准值约40%. 近年来金属纳米结构中洛伦兹数的实验测量结果出现较大差异. 以金纳米薄膜和银纳米线的洛伦兹数测量值为例, 2006—2020年间大量的实验测量工作既发现了高于标准洛伦兹数的结果[57,58,62,63], 也发现了低于标准值的结果[21,59,60,64–66]. 2021年Hu等[67]通过第一性原理计算得到了金和钨中电子和声子模态的导热物性, 结合玻尔兹曼方程, 对金和钨纳米结构的洛伦兹数进行了计算分析. 研究发现室温下金纳米薄膜的声子导热贡献占比低于3%, 洛伦兹数如图5(b)中红色区域所示, 相对标准值的偏离小于40%. 研究同时发现金和钨纳米结构中声子对热导率的贡献比例与体块中的数值差异很大, 且对温度、尺寸敏感. 以上关于导热和洛伦兹数的研究结果均为悬空金属纳米结构的实验和理论结果, 然而很多实际应用中, 金属纳米结构需要在基底上使用. 2013年Lin等[58]实验上发现基底可导致金纳米薄膜热导率下降60%. 2021年Dong等[68]发现在相同基底上厚度分别为40.5, 66.3, 115.8 nm的金纳米薄膜之间电导率的差异接近一个数量级, 而热导率间的差异相对较小, 室温下分别为87, 90, 105 W/(m·K), 尺寸效应相对较弱. 综上所述, 铜、金、银纳米结构中热导率的尺寸效应得到了大量实验和理论的研究, 且现有理论可用来定量解释热导率随尺寸的变化. 而金属纳米结构洛伦兹数的实验测量结果出现了较大差异. 理论计算表明金属纳米结构的洛伦兹数与声子对导热的贡献占比和非弹性散射有关, 其中金纳米薄膜的结果表明其洛伦兹数相对标准值的偏离应在40%以内. 此外, 基底可进一步降低金属纳米结构的热导率, 并可影响电导率和热导率的尺寸效应. 

图 5  (a)铜纳米薄膜理论计算与实验测量的热导率和薄膜厚度的关系[56]; (b)金纳米薄膜的理论计算与实验的归一化洛伦兹数随温度的变化[67]

Fig. 5.  (a) Calculated and experimental thermal conductivity with respect to thickness of copper nanofilm[56]; (b) the calculated and experimental normalized Lorenz number for gold[67].

下载: 全尺寸图片 幻灯片

二维材料的成功制备使其应用成为了可能, 二维材料导热的研究也逐渐成为一个重要方向. 其中二维金属导热的研究仍在起步阶段. 2019年Huang等[69]对二维金属性Nb2C进行了计算并发现声电散射可使声子热导率下降数倍. 研究表明其声电散射作用可以反映在声电散射相空间上. 2022年Wang等[70]对3种金属性MXene, 即Ti2CF2, Ti2CCl2, 和Ti2C(OH)2进行了计算分析. 研究发现热导率范围为54.3—104.7 W/(m·K). 电子和声子作为热载流子在导热中同等重要, 其中电子导热对总热导率的贡献范围为37%—61%. 另一方面, 二维金属性MXene在室温下的洛伦兹数要低于标准值15%左右. 整体上看, 现有的二维金属导热的研究仍较为零散, 有待进一步的探究. 

3.   温度、压强与磁场对金属导热的影响

3.1   温度的影响

金属作为重要的结构材料, 在不同的温度环境下均有着广泛的应用. 温度会改变电子和声子的分布, 影响传热中的载流子的相互作用, 从而影响热导率. 定性理论分析[6,71]与大量定量计算[24,33,36,42,44,45]均表明, 200—800 K下金属中的电子热导率趋于定值. 这是因为随温度上升, 电子比热容的上升与弛豫时间的下降对电子导热的作用相互抵消. 金属中声子导热随温度的变化则如上文讨论, 体现在三声子散射和声电散射的相对强弱上. 近年来金属导热受温度影响的重要成果体现在威德曼-弗朗兹定律上. 威德曼-弗朗兹定律在室温及以上区域是基本成立的, 且多数金属的洛伦兹数相对标准值的偏差低于10%[6,34]. 然而在中低温区洛伦兹数随温度的变化规律则较为复杂. 实验上发现金属铜的洛伦兹数在0 K附近接近标准值, 而在10—100 K附近则可低于标准值60%[20,72]. 0 K附近因电子散射过程中电子与杂质的弹性散射占主导, 因而测得的洛伦兹数与标准值是一致的. 为揭示洛伦兹数在中低温下偏离标准值的机理, 2019年Lavasani等[71]结合了德拜模型与理论推导, 考虑电子在导电和导热过程中不同的散射机制, 对两种过程使用了不同的计算形式. 结果表明, 在室温及以上的温度范围内, 导热和导电过程的电子散射率是相同的; 然而在低于这一温度时, 导热过程的电子散射率要高于导电过程的电子散射率. 因此得到了中低温区洛伦兹数低于标准值的结论, 与实验相一致. 但是, 上述结论为定性的推导和计算, 无法和实验结果进行直接定量对比. 2020年Li等[26]通过第一性原理计算对洛伦兹数的温度变化规律进行了定量分析. 该研究推导了散射率计算的公式, 并认为计算电导率时应使用动量弛豫时间(MRTA), 而计算热导率时应使用能量弛豫时间(ERTA). 通过对比ERTA, MRTA以及Allen模型计算得到的铝和铜的电导率和热导率, 证实了上述弛豫时间的选取方法. 其中铜的电导率和热导率如图6(a), (b)所示, 与实验值吻合良好. 值得注意的, 是中低温下铜的电子热导率和电导率均随温度降低迅速增大, 这是因为低温时, 电子的弛豫时间随温度下降而急剧上升. 据此, 该研究获得了如图6(c)所示的中低温下洛伦兹数随温度的变化关系, 并对比了不同方法和模型的结果. 进一步, 该研究对电子的散射过程进行了分析. 如图6(d)所示, 大散射角度的弹性散射与小散射角度的非弹性散射均可对电子热输运产生影响, 但只有大散射角度的弹性散射会对电输运产生明显影响. 中低温下激发的声子多为低频长波声子, 因此电声散射中非弹性散射的比例上升. 电流输运相较于热流输运受到的抑制作用较小, 导致洛伦兹数低于标准值. 综上所述, 在中低温区, 金属中电输运与电子热输运过程中不同的散射机制导致了洛伦兹数相对标准值的偏离. 这一结论在理论模型与单质金属的计算中得到了验证. 

图 6  考虑MRTA, ERTA计算的铜的(a)电子热导率和(b)电导率[26]与Allen模型结果的对比; (c) MRTA, ERTA, 常弛豫时间近似(Constant), Allen模型和布洛赫-格律乃森模型(BG)计算得到的铜的洛伦兹数的对比[26]; (d)外电场与温度梯度下电子的散射过程, 实心圆代表占据的电子态, 空心圆代表未占据的电子态[26]

Fig. 6.  Calculated (a) electron thermal conductivity and (b) electrical conductivity of copper considering MRTA and ERTA[26], compared with the results from the Allen model; (c) the calculated Lorenz number by MRTA, ERTA, constant relaxation time approximation (Constant), Allen model, and the BG model for Cu[26]; (d) the electron scattering in an electric field and under a temperature gradient[26]. Note that the filled small spheres are occupied electron states and the open small spheres are unoccupied electron states.

下载: 全尺寸图片 幻灯片

3.2   压强的影响

作为重要的结构材料, 金属在很多工程中往往工作在应力条件下. 此外, 压强作为调控金属热导率的重要手段也受到了广泛的关注和研究. 然而在实验上, 维持高压强的同时进行热导率测量有一定的困难. 金刚石铁砧腔测量法可在数百个GPa下进行实验, 但实验复杂, 实现难度大[73]. 理论研究方面, 在20世纪80年代, Bohlin[74]考虑金属中的电子导热, 通过结合布洛赫-格律奈森模型和自由电子气模型推导了金属热导率随压强的变化规律. 研究发现增大压强会减弱电声相互作用, 电子弛豫时间延长, 导致热导率增大. 2019年Giri等[75]通过第一性原理计算电声相互作用及电子热导率, 发现符合自由电子气模型的金属铝、金、银的热导率随压强增大而增大, 这和Bohlin模型的规律一致. 2019年Gomi和Yoshino[76]基于柯林加-科恩-罗斯托克(KKR)格林函数方法结合相干势近似(CPA), 使用久保-格林伍德方法计算了大量不同温度与压强下金属铂的电子热导率, 并发现了其热导率随压强增大而增大. 虽然这种计算方法可以快速获得大量的数据, 然而难以获得诸如电子弛豫时间等微观信息. 2022年Giri等[77]进一步研究了铝的热导率受压强的影响. 如图7(a)所示, 研究发现随压强增大, 铝的热导率增大速度要快于高导热半导体材料. 此外, 铝在200 GPa的压强下热导率可达2000 W/(m·K). 为了更好理解压强对导热的影响机制, 2022年Zhang等[78]通过第一性原理对3种典型金属铝、钨、铂的热导率-压强关系进行了对比分析. 研究发现虽然铝、钨、铂的电子热导率均随压强增大而增大, 但机制并不相同. 如图7(b)所示, 对于铝这种自由电子金属而言, 电子热导率随压强增加的原因是电声相互作用强度下降. 铂和钨是费米能上d轨道电子较多的过渡金属, 图7(c)以钨为例进行分析. 首先, 钨的热导率随压强增大的增幅不如铝大. 其次, 钨电子热导率随压强上升的主要原因是电子群速度的上升; 而电子弛豫时间随压强变化有限, 表明电声相互作用不是主导因素. 此外, 这一工作发现铝、钨、铂的声子热导率同样随压强上升而上升. 综上所述, 自由电子金属的热导率随压强增加的增幅较大, 原因是电声相互作用减弱; 费米能包含d轨道电子的过渡金属的热导率随压强增大的增幅较小, 上述机制与电子群速度有较大关联. 非单质金属以及费米能包含更复杂轨道成分的金属中, 热导率随压强的变化关系有待进一步的探索研究. 

图 7  (a)铝、金刚石、立方氮化硼和砷化硼的热导率随压强的变化[77]; (b)铝、(c)钨的归一化电子热导率、平均速度、弛豫时间和总电子比热容随压强的变化[78]

Fig. 7.  (a) Variation of thermal conductivity with pressure for aluminum, diamond, cubic boron nitride, and boron arsenide[77]; normalized electron thermal conductivity, averaged velocity, relaxation time, and total electron specific heat of (b) Al and (c) W as a function of pressure[78].

下载: 全尺寸图片 幻灯片

3.3   磁场的影响

磁场对金属热导率的影响在实验上有重要意义. 一般认为在2—60 K附近的温区, 施加数个特斯拉的磁场可显著抑制电子热导率, 同时对声子的热导率影响可忽略. 因此在实验上可以通过这种方式来分离出金属中的声子热导率[12,72]. 为研究磁场强度对电子热输运的影响, 1996年Gregg和Haar[19]基于自由电子气模型进行了推导, 并获得了金属中电子热导率随磁场强度变化的解析关系式, 结果表明电子的热导率随磁场强度增大而下降, 且磁场对电子导热的抑制效果与电子平均自由程正相关. 在平均自由程10—100 Å的情况下, 数个特斯拉的磁场强度对电子热导率的作用可忽略. 2016年Yang等[79]通过第一性原理计算定量研究了磁场对铝、镍和铌的电子弛豫时间和热输运性质的影响. 研究发现铝、镍、铌在布里渊区中的电子分布存在差异, 因此电子与磁场的耦合方式不同. 此外, 铌中出现了电子热导率随磁场强度增大而增大的现象, 300 K下, 500 T的磁场强度可使电子热导率上升10%. 以上研究表明如果通过磁场改变金属的热导率, 磁场强度需达到数个特斯拉. 这一强度接近实验极限, 未来的研究中若能降低这一磁场强度将会带来重大的应用价值. 

4.   总结与展望

基于理论与计算的进步, 现阶段对金属导热的定量研究进展迅速. 本文梳理了近年来金属导热理论与计算领域的重要研究成果. 金属中声子对导热的贡献比例一直是研究的重点, 研究发现这与金属类型有一定的关联. 金、银、铜、铝中声子对导热的贡献比例低于5%, 部分过渡金属中这一比例可超过10%. 金属间化合物的声子导热贡献比例与原胞的复杂度有关, 而金属性陶瓷中声子导热贡献占比约为26%—74%. 声子导热的贡献使得部分金属如钨、氮化钛的洛伦兹数高于标准值. 另一方面, 金属的洛伦兹数在室温以上普遍趋于稳定, 而在中低温区时则低于标准值, 这是因为电输运与电子热输运过程中有不同的散射机制. 纳米尺度下金属导热的情况十分复杂, 涉及晶界、边界等多种散射机制, 仍处于探索与发掘阶段. 压强与磁场对金属热导率的影响与具体的电子结构有较大关联, 相关的理论计算近年来得到了一定程度的发展, 为未来金属热导率调控设计等方面提供了支撑. 在未来的金属导热研究中, 实验上, 更好地合成与表征金属纳米材料的导热性质仍是重点研究方向. 理论上, 除了上述的内容与方向, 以下内容可能成为未来研究的重点. 

金属导热中的物理问题. 1)金属中热载流子的多种散射机制. 除了电声散射和三声子散射外, 热载流子还会受到各种界面、边界、位错、原子空位等的散射作用. 建立计算理论框架与探索相关机制一方面可以扩展现有的金属导热基础理论, 另一方面也可揭示不同加工工艺对金属导热的影响机理. 2)非晶金属的导热机制. 非晶金属又名金属玻璃, 其硬度强度相较晶态金属更高. 但因这种金属的原子为无序堆积, 常规基于平面波展开的第一性原理计算难以施加周期性边界条件. 另一方面, 非晶半导体的导热理论已有很大发展, 并建立了基于热传播子、局域子等的多种导热理论. 然而这些机制均针对原子的振动, 非晶金属中的电子如何传递, 如何与原子振动相互作用而影响导热有待进一步探讨. 3)液态金属的导热机制. 液态金属是重要的核电冷却剂, 相较固态金属而言其原子间作用力更弱. 在这种情况下, 电子在输运中受到的散射机制、原子运动对导热的贡献, 以及不同掺杂对液态金属导热的影响机制均有待进一步探索. 

金属导热的设计与调控问题. 1)合金的导热设计. 合金相较纯金属强度更高, 是应用广泛的结构材料. 但合金的热导率相较纯金属低, 这是因为合金中有很多的析出低热导率第二相、且热载流子会受到固溶原子以及界面的散射. 平衡设计高强度和高导热合金是有较大应用价值的学科交叉问题. 2)微纳结构的金属导热设计. 微纳尺度热测量实验、芯片内传热等情况, 需要考虑其中金属导热的尺寸效应. 虽然已有大量实验理论工作开展, 但是如何通过设计微观结构, 调整金属内部成分等方式控制尺寸效应, 按需求设计整体金属的导热研究现在仍开展较少, 这一设计问题有待进一步研究.