一流产品,以专业铸造辉煌


1. 引 言
中国散裂中子源(CSNS)反角白光中子源(Back-n)是我国第一个高通量、宽能区、脉冲化的白光中子源, 其主要用途是开展核数据测量, 基础物理实验和核技术应用[1-4]. Back-n的布局图如图1所示, 高能质子(1.6 GeV)在轰击散裂靶前经过偏转磁铁偏转15°, 这使散裂靶上相对质子束流180°方向出射的中子束与质子输运线有15°夹角, 从而有足够的空间建设反角白光中子束线. 反角白光中子束线全长约80 m, 包括中子输运线和两个实验终端, 其中终端1距离散裂靶约55 m, 终端2距离散裂靶约76 m. 中子输运线包含真空管道、中子束窗、中子开关、中子准直器和废束站. 通过调节中子准直器的准直孔径, 可以在实验终端得到不同几何尺寸的中子束斑, 用于开展不同的物理实验.
CSNS于2018年5月完工, Back-n也于同期建设完成并开展了中子束流参数测量[5-7]. 测量结果表明, Back-n的中子束在1.0 eV—50 MeV都有较高的注量率, 当CSNS运行在100 kW功率时, 实验终端1的中子注量率为1.75 × 107 s–1·cm–2, 实验终端2的中子注量率为7.03 × 106 s–1·cm–2. 目前, CSNS的脉冲束具有双束团和单束团两种模式, 在单束团模式下, Back-n终端2的1 MeV以下中子的时间分辨率好于1%[4]. 较高的中子注量率和较好的时间分辨率, 使Back-n成为优秀的中子物理实验平台. 在完成束流参数测量实验后, 在Back-n上开展了中子俘获截面、全截面[8]、裂变截面[9]、带电粒子产生截面[10,11]、非弹性散射截面等实验测量. 然而, 在这些实验中所有对伽马射线灵敏的探测器, 如闪烁体探测器和高纯锗探测器等, 都受到了束内伽马射线的影响. 特别是中子俘获反应截面测量实验, 部分中子能区的伽马本底占总计数的50%以上, 直接影响了实验结果的精度. 因此需要开展束内伽马射线的研究.
本文从Monte-Carlo(蒙特卡罗)模拟和实验测量两个方面介绍Back-n束内伽马射线的研究结果. 通过蒙特卡罗模拟得到了束内伽马射线的能量分布和时间结构, 通过实验测量得到了低能中子区的束内伽马射线的时间结构, 验证了蒙特卡罗模拟的结果.
2. 蒙特卡罗模拟
蒙特卡罗模拟是研究核反应和粒子输运问题的重要手段, 目前主要的大型粒子输运程序包括MCNP[12], Geant 4[13], Fluka[14]等. Geant 4因其开源设计和强大的几何建模能力而被越来越多地应用到大型射线装置设计和物理实验计算中. 本工作使用Geant 4模拟1.6 GeV质子轰击散裂靶的过程, 跟踪中子和伽马射线的产生和输运过程, 记录从反角方向出射的伽马射线(中子)的能量和时间, 从而得到反角的伽马射线(中子)的能量分布和时间结构.
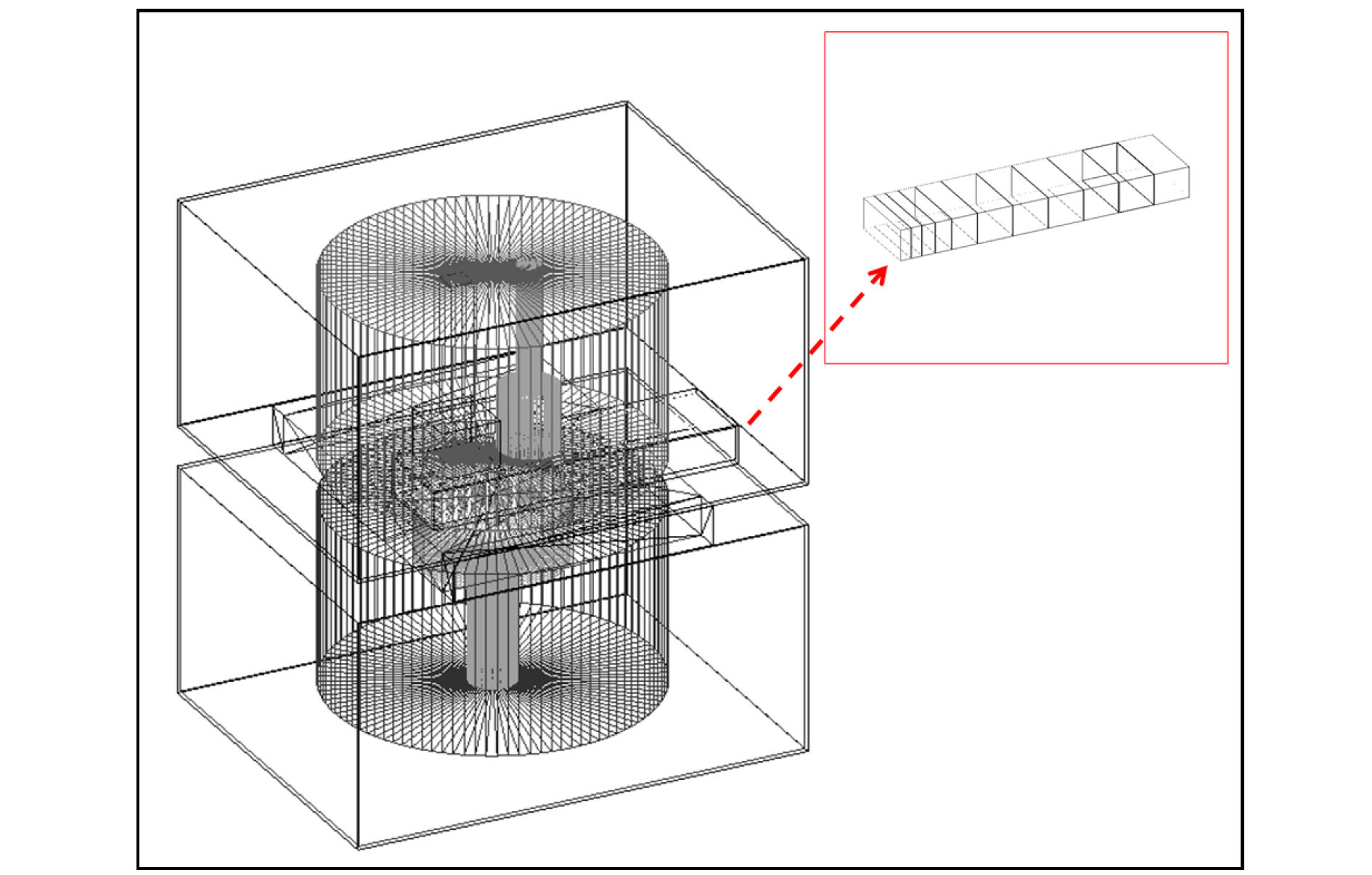
由文献[15]可知, 散裂靶全长65 cm, 由11片钨靶组成, 每片钨靶外包裹0.3 mm的钽, 靶片之间有冷却水. 靶容器为SS316型不锈钢, 质子入射面的厚度为2.5 mm. 在散裂靶的上下还有耦合氢和退耦合氢慢化体, 以及Be-Fe中子反射层. 根据这一几何描述, 使用Geant 4构建了如图2所示的散裂靶几何模型. 其中钨靶主体位于中心位置(框图所示), 上下各有Fe反射体(方形)和Be反射层(圆柱形), Be反射层内部有液氢慢化体和水慢化体.
Geant 4的特色之一在于用户可根据研究对象选择合适的物理模型. 本工作中的模拟计算均采用Geant 4的10.2.p01版本, 选取的Geant 4的物理过程如表1所列, 其中中子核反应数据库使用ENDF/B-VII.1[16].
| 粒子类型 | 能量区间/MeV | 物理模型 |
| 质子 | < 1600 | G4HadronModel |
| G4CascadeInterface | ||
| 中子 | < 20.0 | G4NeutronHPModel (ENDF/B-VII.1) |
| > 20.0 | G4HadronModel | |
| 伽马 | > 0 | G4RayleighScattering |
| G4PhotoElectricEffect | ||
| G4ComptonScattering | ||
| G4GammaConversion | ||
| 电子 | > 0 | G4eMultipleScattering |
| G4eIonisation | ||
| G4eBremsstrahlung |
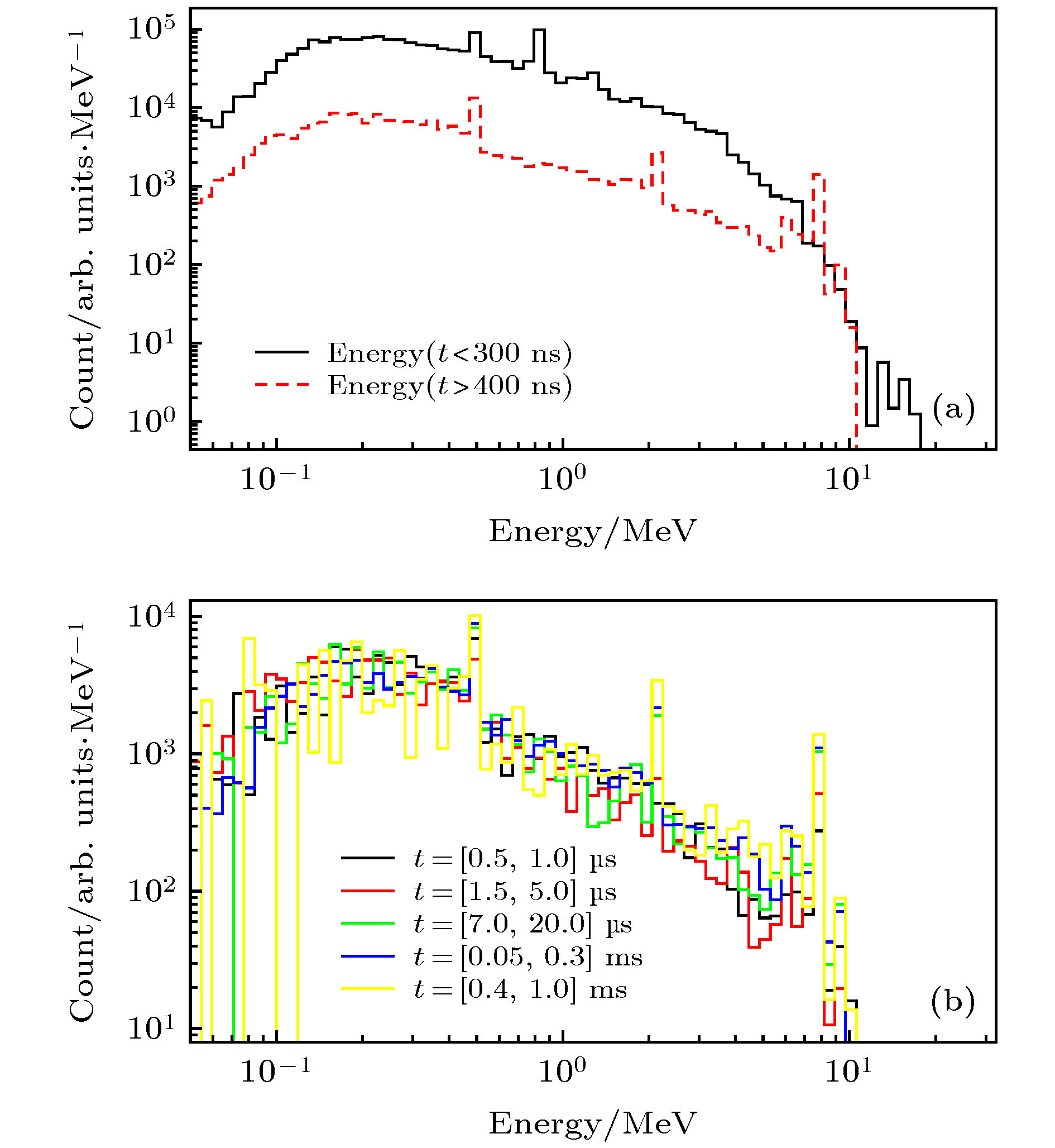
研究Back-n实验终端内的束内伽马射线, 最为直接的方式是构建整个Back-n的几何模型, 在实验终端记录伽马射线的信息. 但是对于80 m长的束线, 以上方法计算效率太低, 耗时太长. 本工作采用分步模拟的方式: 第一步在散裂靶的反角方向2.0 m处设置虚拟探测器, 记录从靶面出射的中子和伽马射线的全部信息, 包括能量、时间、位置和动量; 第二步以这些粒子为源粒子, 抽样到Back-n的实验终端2 (76.5 m). 图3显示了76.5 m处的伽马射线的能量分布(图3(a))和时间分布(图3(b)). 从图3可以看出, 束内伽马射线在20 MeV以下均有分布, 并有明显的特征伽马峰, 如0.511和0.847 MeV. 束内伽马射线的时间结构明显分为两个部分: 在质子打靶后300 ns以内到达实验终端2的伽马射线主要是在散裂反应过程中产生的瞬发伽马, 通常被称为γ-flash, 约占全部束内伽马的91.3%; 之后约2.0 ms内有连续的伽马射线到达实验终端2, 这些伽马大多是中子核反应和散裂反应产物核衰变产生的, 占伽马总量的8.7%. 由于γ-flash和后续的束内伽马射线产生机制不同, 其能谱也会有一定的差异, 图4(a)给出了γ-flash的能谱结构(黑色实线)和连续伽马的能谱(红色虚线). 可以看到, 连续伽马能谱中除0.511 MeV伽马峰外, 还包含了H俘获中子后放出的2.23 MeV的伽马射线和靶材料(W, Ta, Fe等)俘获中子后放出的7.0—10.0 MeV的级联伽马射线. 同样, 对连续伽马也进行了不同时间区间的划分, 为了便于比较, 对每个时间窗内的计数进行了归一. 图4(b)给出不同时段的伽马能谱, 可以发现这些伽马能谱基本一致. 能谱一致极大地简化了实验测量方法, 因为可以忽略探测器对不同时刻伽马射线的探测效率变化.
3. 实验测量
一个脉冲周期内不同时间区间的束内伽马射线对中子物理实验的影响是不同的. γ-flash主要影响高能中子区, 连续伽马射线影响10 eV以上能区. 由于γ-flash的瞬时注量率极高, 大多数伽马灵敏探测器在γ-flash到达时都会产生饱和信号, 随后在1—20 μs内处于恢复期, 恢复期内探测器不能正常输出信号. 因此, 目前测量束内伽马射线完整的时间结构很难做到, 本工作测量了质子打靶12 μs之后的束内伽马射线的时间结构, 重点解决中子俘获截面测量实验中关心的伽马本底问题.
3.1 直接测量法
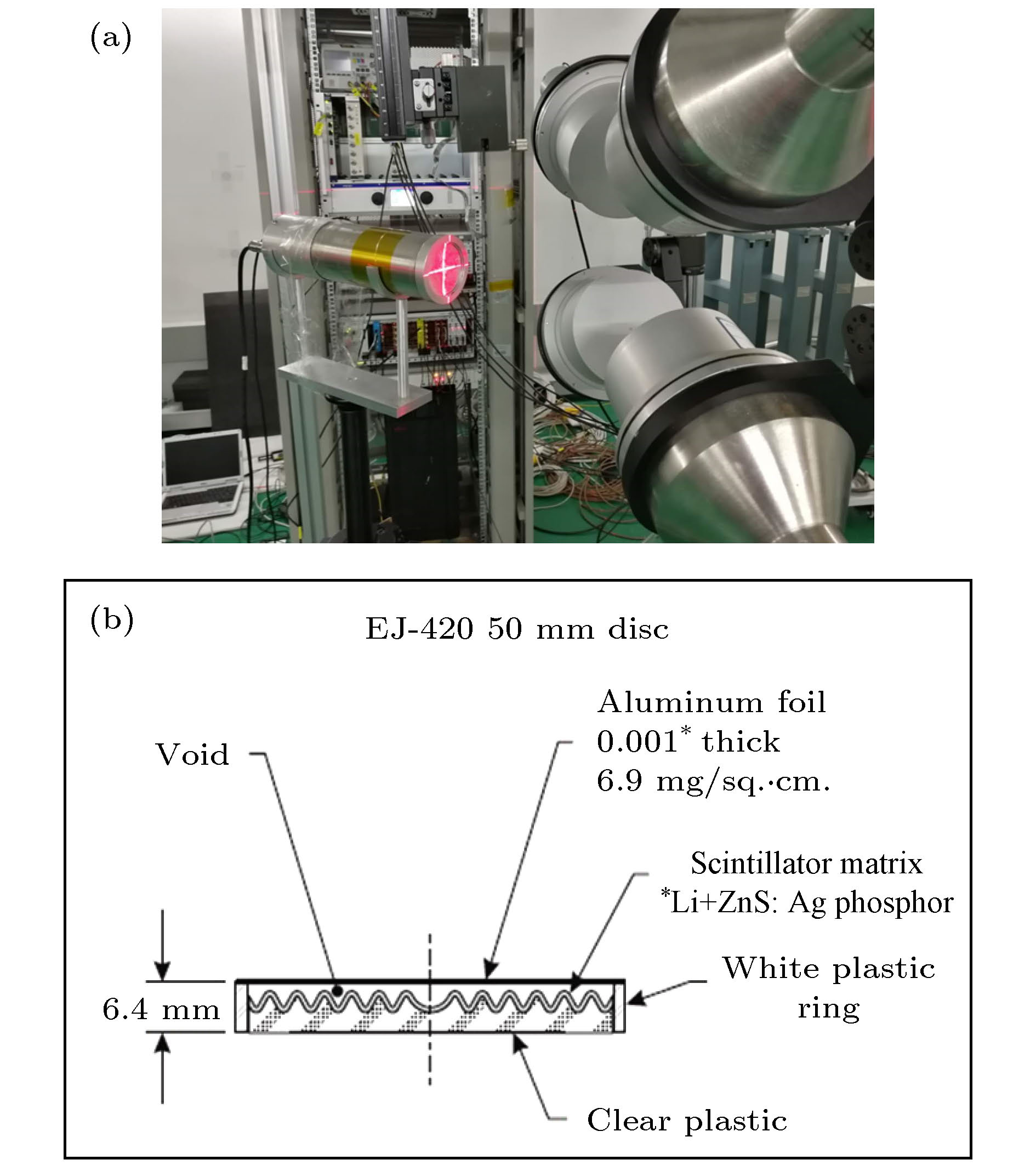
Back-n束内伽马射线时间结构的直接测量实验在终端2进行. CSNS运行在双束团模式, 打靶功率40 kW, Back-n的中子准直孔径组合为12 mm-15 mm-40 mm. 实验现场布局如图5(a)所示. 将载6Li的ZnS(Ag)闪烁体探测器放置在束线上, 探测器前表面距离散裂靶表面76.50 ± 0.05 m, 探测器与束流方向夹角约40°以降低γ-flash对探测器的冲击. ZnS (Ag)闪烁体的型号为EJ-420[17], 其闪烁体结构如图5(b). 闪烁体耦合在光电倍增管上(PMT), PMT的阳极信号直接输入数据获取系统(DAQ)中. DAQ采用Back-n的全波形数字化数据获取系统, 具有1 GS/s采样率, 12 bit分辨率以及37 ms的采样深度, 能够几乎无系统死时间地记录下一个脉冲周期内的所有信号[18]. 此外, 在终端1(57.5 m)放置了一片181Ta和一片59Co, 厚度都为1.0 mm, 用于吸收特定能量的中子, 以定量分析束内伽马射线[19].
EJ-420一般用于测量300 keV以下的中子, 但实验表明EJ-420对伽马射线也有明显的响应, 且伽马射线和中子产生的信号的幅度和衰减时间显著不同. 图6给出实验测得的EJ-420的伽马信号和中子信号的波形, 可以看出伽马信号具有较快的衰减时间和较小的峰面积, 能够利用电荷比较法甄别出伽马信号和中子信号. 电荷比较法是根据信号的快慢成分不同进行粒子甄别, 通常需要将信号的不同区域积分. 将EJ-420的每个波形的峰值前后20 ns区间作为Pre-Gate, 峰值后的200—400 ns区间作为Post-Gate, 分别求出两个区间的峰面积并统计二维谱, 如图7(a)所示. 伽马射线由于幅度低、衰减快, 因此集中在图7(a)的左下方, 伽马信号的Post-Gate积分出现负值是由于在这一积分区间很多伽马信号已经衰减到基线, 在减基线过程中由于基线涨落而产生负值. 中子信号由于幅度大、衰减慢都分布在图7(a)的右侧.
束内伽马射线的时间结构通过飞行时间法确定[15]:
|
TOF=(tm−tγ-flash)+L/c.TOF=(tm−tγ-flash)+L/c. |
(1) |
通过过阈定时法(5 mV)确定γ-flash到达探测器的时间tγ-flashtγ-flash, 以及每个阳极信号的触发时间tm, 然后根据散裂靶表面到探测器表面的距离L和光速c可以确定该信号的飞行时间TOF.
图7(b)给出了不同粒子甄别条件下的飞行时间(TOF)谱. 其中黑色实线表示所有信号(中子和伽马)的TOF谱, 红色虚线表示仅有伽马信号的TOF谱. 从包含中子的TOF谱上可以明显看到181Ta吸收片的吸收谷, 吸收谷的谷底恰好落在伽马TOF谱的上面, 验证了粒子甄别的准确性. 同时, 从图7(b)中还可以直观地看到γ-flash对EJ-420探测器的影响: 6 μs之前, 探测器受γ-flash和高能中子信号的影响处于饱和状态, 输出信号异常; 6—20 μs中探测器逐渐恢复正常, 可以看到6Li(n, t)4He核反应在240 keV的共振峰; 20 μs以后探测器处于正常工作状态. 因此, 直接测量法可以得到20 μs之后的束内伽马的时间结构, 对应中子能量为75 keV以下.
3.2 间接测量法
伽马射线的能谱在不同时刻基本一致, 不同时刻在同一样品上的散射伽马粒子的数量能够反映该时刻入射伽马射线的强度. 因此, 可以通过间接测量样品上的散射伽马粒子确定束内伽马射线的时间结构. 由于待测时间区间对应的中子能量较低, 在选择样品时应当挑选伽马散射截面大, 中子俘获截面和弹性散射截面小的核素. 208Pb具有以上特征, 是非常理想的核素, 本工作中使用天然铅(natPb)代替208Pb. 探测器的选择同样非常重要, 低能中子容易被探测器上的材料俘获, 靶核俘获中子后放出的级联伽马射线数量多、能量高、极易影响伽马测量. 特别是含氢探测器, 氢俘获中子后放出的2.23 MeV的伽马射线是较大的干扰. C6D6探测器是用氘替代氢的液体闪烁体探测器, 其俘获中子的概率大大低于含氢闪烁体探测器, 被广泛用于中子俘获截面测量实验. 利用Back-n上的C6D6探测器系统[20]和natPb样品开展了Back-n束内伽马射线的时间结构测量, CSNS工作状态与直接测量实验一致, 现场布局如图8(a). 直径40 mm, 厚度1 mm的natPb置于束流线上, 与直接测量法中EJ-420闪烁体的位置一致. 4个C6D6探测器位于样品上游方向, 探测器轴线与束流方向夹角约110°, 探测器中心距离样品中心约15 cm. 探测器的PMT阳极信号输入Back-n的DAQ系统进行波形采集. 实验中能够通过测量空样品扣除与natPb样品无关的中子和伽马本底, 但样品上散射的束内伽马和中子在样品上诱发的伽马信号无法通过实验方法扣除, 需要借助蒙特卡罗模拟. 模拟程序同样使用Geant 4, 物理模型和数据库与表1中一致. 在模拟程序中中子束流由散裂靶表面抽样至样品处, 源中子能谱使用实验测量的Back-n的中子能谱[5-7]. Geant 4程序中详细描述了探测器几何尺寸和材料, 记录到达探测器灵敏区的伽马射线的时刻和沉积能量. 图8(b)为使用Geant 4构建的探测器和样品的几何模型.
虽然C6D6探测器位于束流外, 但在样品上散射的γ-flash仍然能够在探测器内产生较大的信号, 这一信号同样可以作为时间参考. 同样采用过阈定时法确定每个信号的触发时间tm, 根据(1)式得到C6D6探测器的TOF谱如图9所示. 图9中黑色实线为扣除无样本底的natPb的TOF谱, 红色实线为Geant 4模拟得到的TOF谱. 在Geant 4模拟中只包含了源中子与natPb样品和探测器的相互作用, 因此Geant 4模拟结果与实验结果的差异主要来源于束内伽马射线. 图9中蓝色虚线为实验TOF谱与模拟TOF谱的差值, 代表了束内伽马射线的时间结构. 间接测量法可以得到12 μs之后的束内伽马时间结构, 对应中子能量为210 keV以下. TOF小于12 μs时, 实验结果受中子影响较大, 数据精度较差.
4. 结果与讨论
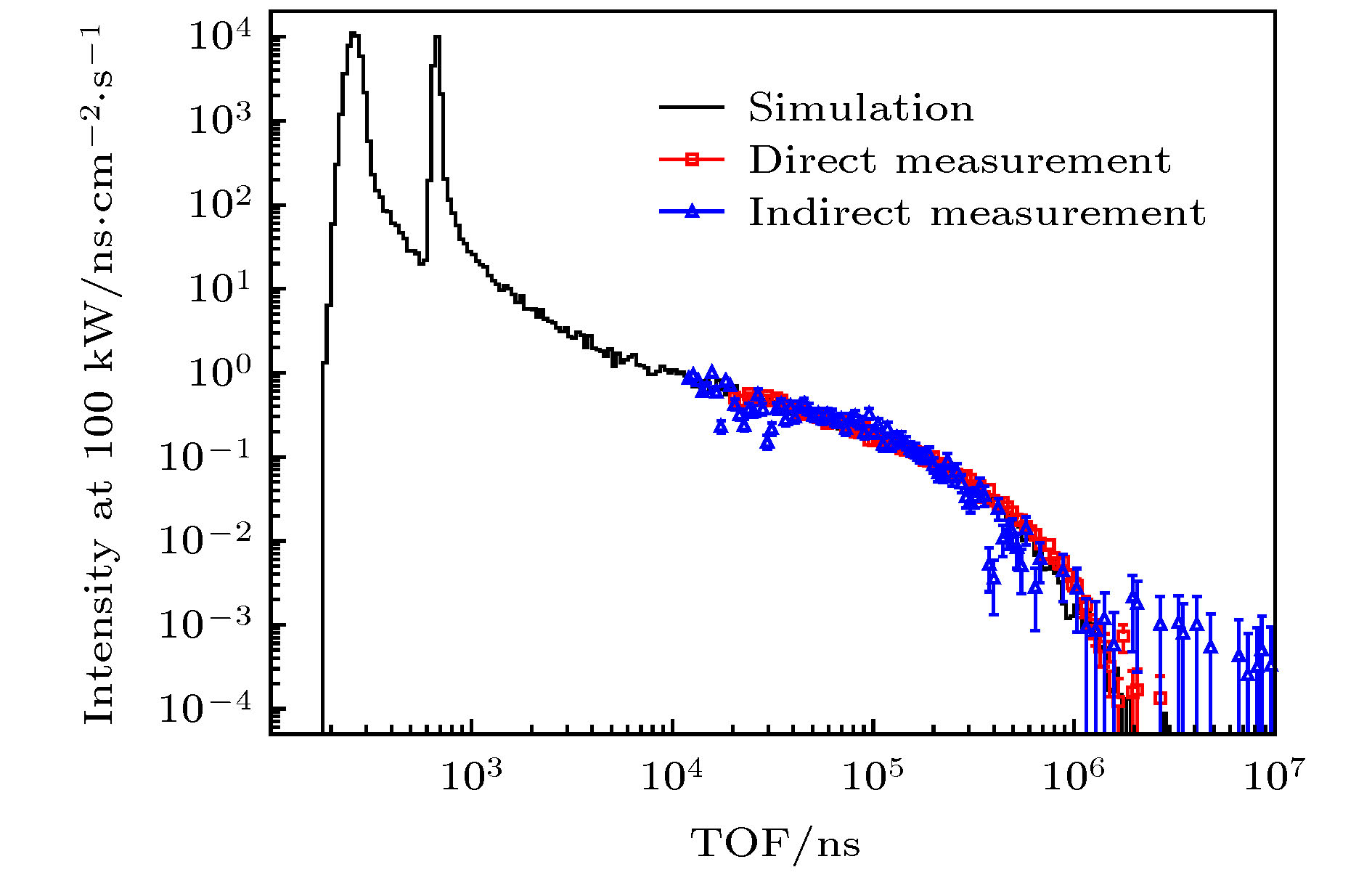
直接测量和间接测量实验能够得到束内伽马射线的时间结构, 但由于探测器的探测效率未知, 无法测得束内伽马射线的注量率. 根据Geant 4模拟结果, 相同位置的中子和伽马射线的注量率的比值为5.8∶1.0. 当CSNS运行在100 kW时, Back-n终端2的中心位置的中子注量率为7.03 × 106 s–1·cm–2[5,6], 那么相同功率下束内伽马射线的注量率约为1.21 × 106 s–1·cm–2. 此外, 实验测量都在CSNS的双束团模式下开展, Geant 4模拟得到的束内伽马射线的时间结构应当包含质子束团的时间结构才能与实验结果进行比较. 双束团模式下, 同一质子脉冲内的两个质子束团时间间隔为410 ns, 单个束团半高宽约为41 ns[3,4], 按照这一参数对模拟谱进行高斯展宽和双束团叠加. 图10给出包含质子束团结构的模拟结果与直接测量结果以及间接测量结果的比较, 其中横坐标按照对数等间距将每个数量级分为50个区间. 模拟谱和实验测量谱的纵坐标计数均归一到100 kW功率时的伽马射线注量率. 测量值的不确定度主要来源于统计不确定度和注量率归一引入的不确定度: 由于束内伽马射线的强度随TOF增大快速降低, 实验测量的统计不确定度由2%逐渐增大到50%以上, 伽马注量率归一引入约8%的不确定度. 由图10可见, 在TOF为20 μs—2 ms时, 蒙特卡罗模拟值与直接测量法的结果在不确定度范围内符合较好; 在12 —20 μs内, 间接测量法的结果也与模拟结果一致. 这表明, Geant 4模拟得到的束内伽马射线的时间结构和能量分布是可信的, 可以用于中子测量实验的伽马本底分析.
5. 结 论
通过蒙特卡罗模拟和实验测量得到了Back-n实验终端2内的束内伽马射线的时间结构. 当飞行时间大于12 μs时, 实验结果与模拟结果符合较好, 对应中子能量为1.0 eV—210 keV. 这为中子俘获反应截面测量实验提供了本底分析的依据. 对于飞行时间小于12 μs的束内伽马射线, 由于探测器受γ-flash和高能中子的影响较为严重, 本工作未能测得其时间结构. 在下一步工作中, 将尝试使用增益较小而线性电流较大的光电倍增管开展直接测量实验, 或是使用门控光电倍增管避开γ-flash的冲击. 此外, 由于探测器对伽马射线的探测效率未知等因素, 本次测量不能确定束内伽马射线的绝对注量率, 只能通过中子注量率和蒙特卡罗模拟得到的中子和伽马的比例间接估算终端2的束内伽马注量率约为1.21 × 106 s–1·cm–2. 但在低能区中子截面测量实验中, 使用181Ta和59Co等吸收片能够定量分析共振能量处的束内伽马本底, 结合本工作得到的时间结构则能定量确定1.0 eV—210 keV中子能区的束内伽马本底.
感谢中国科学院高能物理研究所敬罕涛副研究员的讨论.

扫一扫
关注我们








 下载:
下载: